Moving Charge & Magnetic Field

Ch.4. Moving Charge & Magnetic Field

OERSTED’S EXPERIMENT:

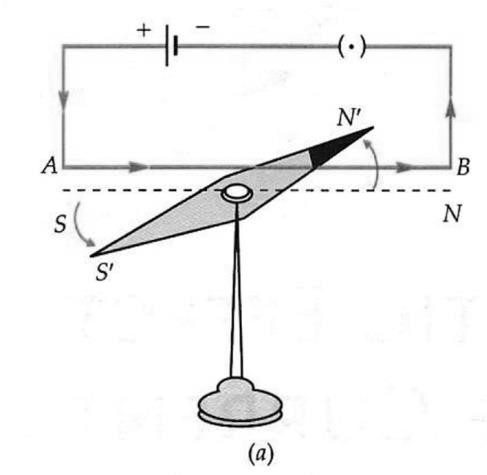
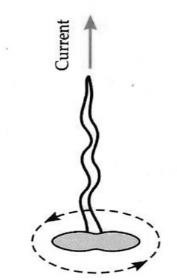
If a magnetic needle SN pivoted over a stand. Hold a wire AB parallel to the needle SN and connect it to a cell and a plugkey, as shown in Fig.

It is observed that:

When the wire is held above the needle and the current flows from the south to the north, the north pole of the magnetic needle gets deflected towards the west, as shown in Fig.(a).
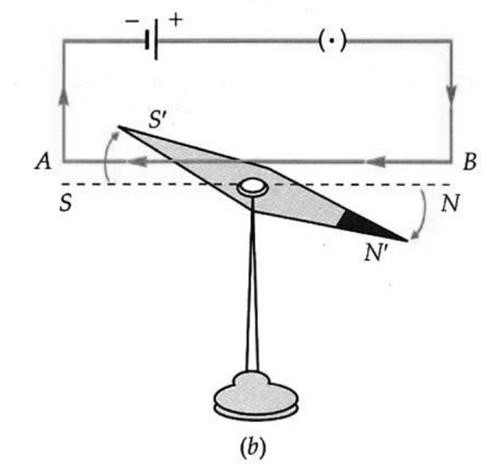
When the direction of the current is reversed, so that it flows from the north to the south, the north pole of the magnetic needle gets deflected towards the east, as shown in Fig.(b).
When the wire is placed below the needle, the direction of deflection of the needle is again reversed.
When the current in the wire is stopped flowing, the magnetic needle comes back into its initial position.

Since a magnetic needle can be deflected by a magnetic field only, it follows from the above experiment that a current carrying conductor produces a magnetic field around it.

Rules for finding the direction of magnetic field due to straight current carrying conductor:

Either of the following two rules can be used for this purpose:

1. Right hand thumb rule. If we hold the straight conductor in the grip of our right hand in such a way that the extended thumb points in the direction of current, then the direction of the curl of the angers will give the direction of the magnetic field.
2. Maxwell’s cork screw rule. If a right handed screw be rotated along the wire so that it advances in the direction of current, then the direction in which the thumb rotates gives the direction of the magnetic field.

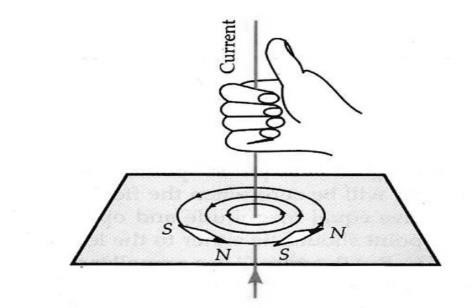
Rules for finding the direction of a magnetic field due to a circular current loop: Either of the following two rules can be used for finding the direction of B.

1. Right hand thumb rule. If we curl the palm of our right hand around the circular wire with the fingers pointing in the direction of the current, then the extended thumb gives the direction of the magnetic field.
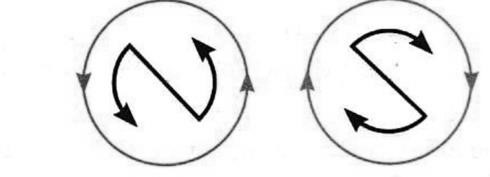2. Clock rule. This rule gives the polarity of any face of the circular current loop. If the current round any face of the coil is in anticlockwise direction, it behaves like a north pole. If the current flows in the clockwise direction, it behaves like a south pole.

FORCE ON A MOVING CHARGE IN A MAGNETIC FIELD:

Lorentz recognized that, the electric charges moving in a magnetic field experience a force, while there is no such force on static charges.

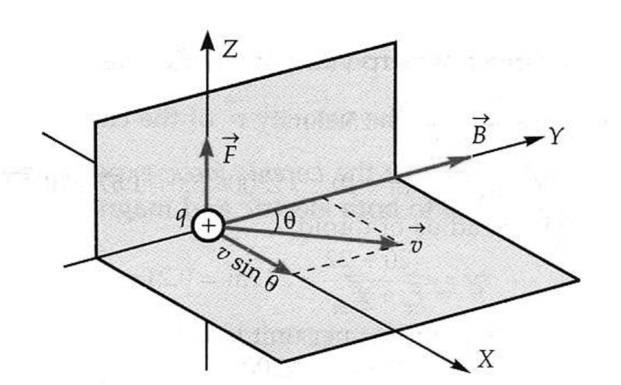
the force is proportional to the magnitude of the magnetic field, i.e., F ∝ B
the force is proportional to the charge q, i.e., F ∝ q
the force is proportional to the component of the velocity v in the perpendicular direction of the field B, i.e., F ∝ v sin θ

Combining the above factors, we get, F ∝ Bqv sin θ

or F = kqvB sin θ

The unit of magnetic field is so defined that the proportionality constant k becomes unity in the above equation. Thus, 𝐅 = 𝐪𝐯𝐁 𝐬𝐢𝐧 𝛉

In vector form the expression can be given as, $\displaystyle \overrightarrow{F}=q\left( {\overrightarrow{v}\times \overrightarrow{B}} \right)$

Clearly the direction of this force will be normal to the plane made by ⃗v⃗ and ⃗B⃗⃗. For positive charge this direction can be determined using Fleming’s left hand rule or using Right hand (palm) rule.

Special Cases:

Case 1. If v = 0, then F = 0 Thus, a stationary charged particle does not experience any force in a magnetic field.

Case 2. If θ =0° or 180°, then F =0 Thus, a charged particle moving parallel or antiparallel to a magnetic field does not experience any force in the magnetic field.

Case 3. If θ = 90°, then F = qvB sin 90° = qvB Thus, a charged particle experiences the maximum force when it moves perpendicular to the magnetic field.

Rules for finding the direction of force on a charged particle moving perpendicular to a magnetic field.

The direction of magnetic Lorentz force $\displaystyle \overrightarrow{F}$ can be determined by using either of the following two rules :

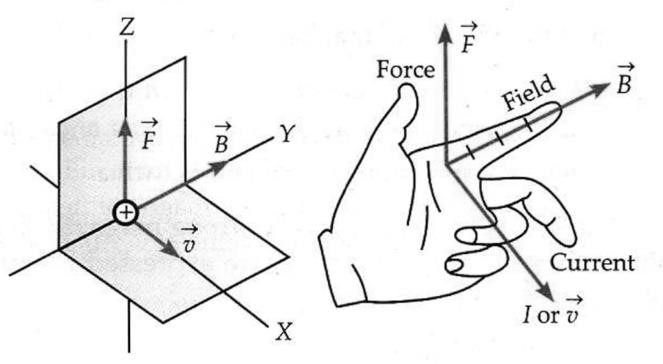Fleming’s left hand rule. Stretch the thumb and the first two fingers of the left hand mutually perpendicular to each other. If the forefinger points in the direction of the magnetic field, central finger in the direction of current, then the thumb gives the direction of the force on the charged particle.

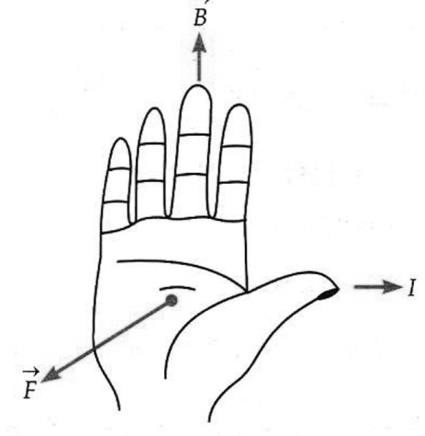Right hand (palm) rule. Open the right hand and place it so that tips of the fingers point in the direction of the field $\displaystyle {\overrightarrow{B}}$ and thumb in the direction of velocity $\displaystyle {\overrightarrow{v}}$ of the positive charge, then the palm faces towards the force $\displaystyle \overrightarrow{F}$ ,

Definition of magnetic field. We know that, B = $\displaystyle \frac{F}{{qv\sin \theta }}$

If q = 1, v = 1, θ = 90°, sin 90° = 1, then B = F

Thus, the magnetic field at a point may be defined as the force acting on a unit charge moving with a unit velocity at right angles to the direction of the field.

SI unit of magnetic field. Again, we use, B = $\displaystyle \frac{F}{{qv\sin \theta }}$

∴ SI unit of B= $\displaystyle \frac{N}{{C.m{{s}^{{-1}}}}}$ = $\displaystyle \frac{N}{{Am}}$ = Tesla (T)

CGS unit of B is Gauss (G). 1 Gauss =10^-4 Tesla

Dimensions of magnetic field. Clearly, $\displaystyle \left[ B \right]=\frac{{\left[ F \right]}}{{\left[ q \right]\left[ v \right]\left[ {\sin \theta } \right]}}$ = $\displaystyle \frac{{ML{{T}^{{-2}}}}}{{AT.L{{T}^{{-1}}}.1}}$ = $\displaystyle \left[ {M{{T}^{{-2}}}{{A}^{{-1}}}} \right]$

LORENTZ FORCE:

The total force experienced by a charged particle moving in a region where both electric and magnetic fields are present, is called Lorentz force.

A charge q in an electric field $\displaystyle \overrightarrow{E}$ experiences the electric force, $\displaystyle \overrightarrow{{{{F}_{e}}}}=q\overrightarrow{E}$

This force acts in the direction of field $\displaystyle \overrightarrow{E}$ and is independent of the velocity of the charge.

The magnetic force experienced by the charge q moving with velocity $\displaystyle \overrightarrow{v}$ in the magnetic field B is given by, $\displaystyle \overrightarrow{F}=\overrightarrow{{{{F}_{e}}}}+\overrightarrow{{{{F}_{m}}}}=q\left( {\overrightarrow{E}+\overrightarrow{v}\times \overrightarrow{B}} \right)$

The total force, or the Lorentz force, experienced by the charge q due to both electric and magnetic field is given by,

$\displaystyle \overrightarrow{F}=\overrightarrow{{{{F}_{e}}}}+\overrightarrow{{{{F}_{m}}}}=q\left( {\overrightarrow{E}+\overrightarrow{v}\times \overrightarrow{B}} \right)$

MOTION OF A CHARGED PARTICLE IN A UNIFORM MAGNETIC FIELD:

When a charged particle having charge q and velocity 𝑣⃗ enters a magnetic field B, it experiences a force, $\displaystyle \overrightarrow{F}=q\left( {\overrightarrow{v}\times \overrightarrow{B}} \right)$ or F = qvB sin θ

The direction of this force is perpendicular to both $\displaystyle {\overrightarrow{v}}$ and $\displaystyle {\overrightarrow{B}}$ .

Following three cases are possible:

When the initial velocity is parallel to the magnetic field. Here θ = 0°, so F = qvB sin 0° = 0. Thus the parallel magnetic field does not exert any force on the moving charged particle. The charged particle will continue to move along the line of force. In this case there will not be any change in magnitude of velocity and kinetic energy of the particle.
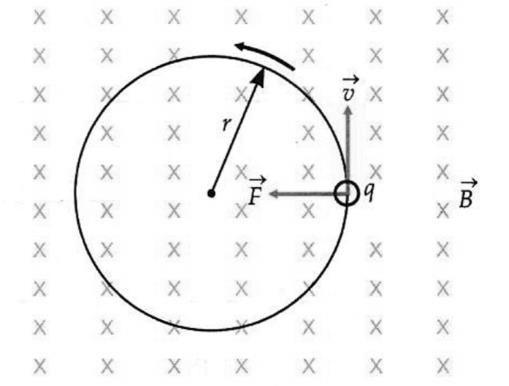
When the initial velocity is perpendicular to the magnetic field.

Here θ = 90°, so F = qvB sin 90° = qvB = a maximum force.

As the magnetic force acts on a particle perpendicular to its velocity, it does not do any work on the particle. It does not change the kinetic energy or speed of the particle.

This force acts on the particle perpendicular to both 𝑣⃗ and

$\displaystyle {\overrightarrow{B}}$ . This force continuously deflects the particle sideways

without changing its speed and the particle will move along a circle perpendicular to the field. Thus, the magnetic force provides the centripetal force.

Radius of the circular Path:

Let r be the radius of the circular path. Then, Centripetal force = Magnetic force, qvB

Or $\displaystyle \frac{{m{{v}^{2}}}}{r}$ = qvB or Radius, r = $\displaystyle \frac{{mv}}{{qB}}$ = $\displaystyle \frac{p}{{qB}}$

Thus. the radius of the circular orbit is inversely proportional to the specific charge q

(charge to mass ratio $\displaystyle \frac{q}{m}$ ) and to the magnetic field.

Period of revolution:

Period of revolution, T = $\displaystyle \frac{{Circumference}}{{Speed}}$ = $\displaystyle \frac{{2\pi r}}{v}$ = $\displaystyle \frac{{2\pi }}{v}.\frac{{mv}}{{qB}}$ = $\displaystyle \frac{{2\pi m}}{{qB}}$

Clearly, the time period is independent of v and r. If the particle moves faster, the radius is larger, it has to move along a larger circle so that the time taken is the same.

The frequency of revolution is, $\displaystyle {{f}_{c}}=\frac{1}{T}=\frac{{qB}}{{2\pi m}}$

This frequency is called cyclotron frequency.

3. When the initial velocity makes an arbitrary angle with the field direction.

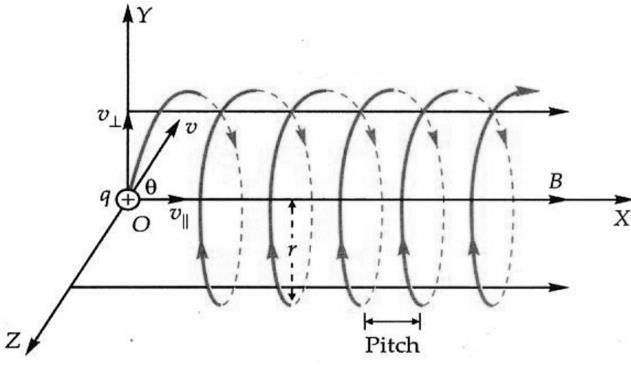A particle of charge q and mass m enters the field $\displaystyle \overrightarrow{B}$ with velocity 𝑣⃗ inclined at angle θ with the direction of the field $\displaystyle \overrightarrow{B}$ , as shown in Fig.

The velocity $\displaystyle \overrightarrow{v}$ can be resolved into two rectangular components:

The component along the direction of the field i.e., along X-axis. Clearly, 𝑣_𝑥= 𝑣 cos𝜃

The parallel component remains unaffected by the magnetic field and so the charged particle continues to move along the field with a speed of v cos θ.

The component 𝑣_𝑦 perpendicular to the direction of the field i.e., in the YZ-plane. Clearly, 𝑣_𝑦= 𝑣 sin𝜃

Due to this component of velocity, the charged particle experiences a force F = qv_y B which acts perpendicular to both v_y and B. This force makes the particle move along a circular path in the YZ-plane. Thus, a charged particle moving in a uniform magnetic field has two concurrent motions, a linear motion in the direction of $\displaystyle \overrightarrow{B}$ (along X-axis) and a circular motion in a plane perpendicular to B (in YZ-plane). Hence the resultant path of the charged particle will be a helical path, with its axis along the direction of $\displaystyle \overrightarrow{B}$ .

The radius of the circular path is, 𝑟 = $\displaystyle \frac{{m{{v}_{y}}}}{{qB}}$ = $\displaystyle \frac{{mv\sin \theta }}{{qB}}$

The period of revolution is, 𝑇 = $\displaystyle \frac{{2\pi r}}{{{{v}_{y}}}}$ = $\displaystyle \frac{{2\pi }}{{v\sin \theta }}.\frac{{mv\sin \theta }}{{qB}}$ = $\displaystyle \frac{{2\pi m}}{{qB}}$

The linear distance travelled by the charged particle in the direction of the magnetic field during its period of revolution is called pitch of the helical path.

pitch = 𝑣_𝑥× 𝑇 = 𝑣cos𝜃 × $\displaystyle \frac{{2\pi m}}{{qB}}$ = $\displaystyle \frac{{2\pi mv\cos \theta }}{{qB}}$

FORCE ON A CURRENT CARRYING CONDUCTOR IN A MAGNETIC FIELD:

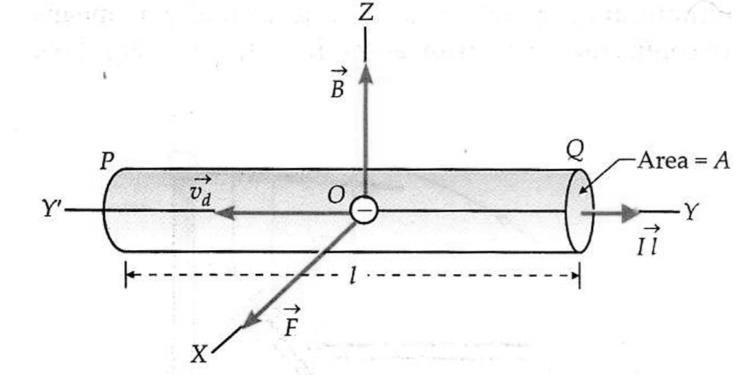As shown in Fig., let us consider a conductor PQ of length l, area of cross- section A, carrying current I along +ve Y-direction. The field $\displaystyle \overrightarrow{B}$ acts along +ve Zdirection. The electrons drift towards left with velocity v_d. Each electron experiences a magnetic

Lorentz force along +ve X-axis, which is given by,

𝑓 = 𝑒𝑣_𝑑𝐵 sin 𝜃

If n is the number of free electrons per unit volume, then total number of electrons in the conductor is, 𝑁 = 𝑛 × 𝑣𝑜𝑙𝑢𝑚𝑒 = 𝑛𝐴𝑙

Total force on the conductor is, 𝐹 = 𝑁𝑓 = 𝑛𝐴𝑙 𝑒𝑣_𝑑𝐵 sin 𝜃 or 𝑭 = 𝑰𝒍𝑩 𝐬𝐢𝐧 𝜽 Where, current, 𝐼 = 𝑛𝐴𝑒𝑣_𝑑

Hence, in vector form, $\displaystyle \overrightarrow{F}$ = 𝐼(𝑙⃗× $\displaystyle \overrightarrow{B}$ ) Special Cases:

If θ=0°or 180°, then 𝐹 = 𝐼𝑙𝐵 (0) = 0

Thus, a current carrying conductor placed parallel to the direction of the magnetic field does not experience any force,

If θ =90°, then, 𝐹 = 𝐼𝑙𝐵𝑠𝑖𝑛90° = 𝐼𝑙𝐵 or 𝐹𝑚𝑎𝑥 = 𝐼𝑙𝐵

Thus, a current carrying conductor placed perpendicular to the direction of a magnetic field experiences a maximum force.

Direction of force. The direction of force on a current carrying conductor placed in a perpendicular magnetic field is given by Fleming’s left hand rule.

BIOT-SAVART LAW: (Magnetic Field due to a Current Element):

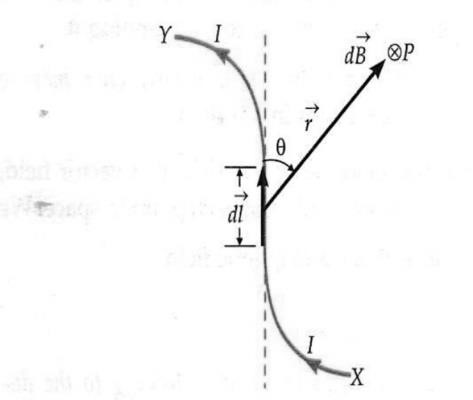Statement. According to Biot-Savart law, the magnitude of

the field $\displaystyle \overrightarrow{{dB}}$ , produced by a current element is

directly proportional to the current I through the conductor, 𝑑𝐵 ∝ 𝐼
directly proportional to the length dl of the current element, dB ∝ dl
directly proportional to sin θ, dB ∝ sin θ
inversely proportional to the square of the distance r of the point P from the current element, 𝑑𝐵 ∝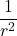 $\displaystyle \frac{1}{{{{r}^{2}}}}$

Combining all these four factors, we get, 𝑑𝐵 ∝ $\displaystyle \frac{{Idl\sin \theta }}{{{{r}^{2}}}}$

or dB = $\displaystyle K.\frac{{Idl\sin \theta }}{{{{r}^{2}}}}$ = $\displaystyle \frac{{{{\mu }_{0}}}}{{4\pi }}$ . $\displaystyle \frac{{Idl\sin \theta }}{{{{r}^{2}}}}$

The proportionality constant K depends on the medium between the observation point

P and the current element and the system of units chosen. For free space and in SI units,

𝐾 = $\displaystyle \frac{{{{\mu }_{0}}}}{{4\pi }}$ = 10^-7 TmA⁻¹( or Wbm⁻¹A⁻¹)

As the direction of dB is perpendicular to the plane of $\displaystyle \overrightarrow{{dl}}$ and $\displaystyle \overrightarrow{r}$ , so from the above equation, we get the vector form of the Biot-Savart law as, $\displaystyle \overrightarrow{{dB}}$ = $\displaystyle \frac{{{{\mu }_{0}}I}}{{4\pi }}.\frac{{\overrightarrow{{dl}}\times {{r}^{2}}}}{{{{r}^{3}}}}$

Direction of $\displaystyle \overrightarrow{{dB}}$ . The direction of $\displaystyle \overrightarrow{{dB}}$ is the direction of the vector $\displaystyle \overrightarrow{{dl}}$ × $\displaystyle \overrightarrow{r}$ . It is given by right hand screw rule.

Special Cases:

If θ =0°, sin θ =0, so that dB=0, i.e., the magnetic field is zero at points on the axis of the current element.
If θ =90°, sin θ =1, so that dB is maximum i.e., the magnetic field due to a current element is maximum in a plane passing through the element and perpendicular to its axis.

Post Views: 37

Moving Charge & Magnetic Field

Leave a Reply Cancel reply