Practical of Physics Class 11

Experiment – 1

Object –

To measure the diameter of a given wire using screw gauge.

Apparatus –

Screw gauze, wire.

Theory-

If with the object between plane faces A and B, the edge of the cap lies ahead of N^th division of linear scale.

Then, linear scale reading (L.S.R) =N

If N^th division of circular scale lies over reference line.

Then, circular scale reading (C.S.R) = n x L.C.

Total reading (TR) = L.S.R + C.S.R = N + n x L.C.

Determination of least count of the screw gauge = 1 L.S.D

= 1mm

Number of full rotations given to screw = 4

Distance moved by the screw = 4mm

No. of divisions on circular scale = 100

Hence,

Least count = = 0.01mm =0.001cm

Diagram

Observations –

Least count of screw gauge = 0.01mm
Error correction = —— mm

Observation Table-

Observation table for diameter (longitudinal)

S.No.	L .S. R.(mm) (x)	C. S. R. (mm)		Total reading (x + y) (mm)	Average reading (mm)
S.No.	L .S. R.(mm) (x)	n	n x L. C.=y	Total reading (x + y) (mm)	Average reading (mm)
1
2
3

Observation table for internal diameter- (Transverse)

S.No.	L .S. R.(mm) (x)	C. S. R. (mm)		Total reading (x + y) (mm)	Average reading (mm)
S.No.	L .S. R.(mm) (x)	n	n x L. C.=y	Total reading (x + y) (mm)	Average reading (mm)
1
2
3

Calculation—

Observed diameter d = $\displaystyle \frac{{{{d}_{1}}+{{d}_{2}}}}{2}$ = ——– = ——mm

Corrected diameter ₌Observed diameter +(error correction)

= ———–+———–mm

=——–mm

Result –

The diameter of the given object is = ……mm

Precautions-

To avoid under pressure ; the screw should always be rotated by ratchet R and not by cap K.
The screw should move freely without friction.
The zero correction with proper sign should be noted very carefully and added algebraically.

Sources of Error –

The screw may have friction.
The screw gauge may have back lash error.
Circular scale divisions may not be of equal size.

Experiment – 2

Object-

To find the weight of a given body using law of parallelogram and law of vectors (forces)

Apparatus Required-

Parallelogram law of forces apparatus(Gravesend’s apparatus), plumb line, three hanger with slotted weights, thin strong thread, white drawing paper sheet, drawing pins, mirror strip, sharp pencil, half meter rod, set squares, protector, a given body, wooden block (whose weight is to be found), spring balance.

Theory-

If the body of unknown weight S suspended from middle hanger, balances weights P & Q suspended from other two hangers, then

P + Q + S = O

Or S = – (P + Q)

S = – R

The unknown weight must have a magnitude equal to the resultant of the other two known weights

Gravesand’s Apparatus.

Observation –

Scale let 1cm = ——-gm

S.No.	Forces		Slides			Resultant Force R (g.wt)	Unknown Weight S	Weight by spring balance (g.wt)	Error
S.No.	P (g.wt)	Q (g.wt)	OA (cm)	OB (cm)	OC (cm)	Resultant Force R (g.wt)	Unknown Weight S	Weight by spring balance (g.wt)	Error
1
2
3									1

Calculations-

Mean unknown weight S = $\displaystyle \frac{{{{s}_{1}}+{{s}_{2}}+{{s}_{3}}}}{3}$ = =

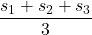Weight of spring balance =

Difference =

Result –

The unknown weight of wooden block = g

The error is within limits of experiment error

Precautions –

The board should be stable & vertical
The pulleys should be frictionless

Sources of Error-

Pulleys may have friction
Weights may not be accurate

Experiment-3

Aim –

To find the force constant of a helical spring by plotting graph between load and extension.

Apparatus Required –

Spring, a rigid support, a 20 g hangar and five 20 g slotted weights, a vertical wooden scale, a fine pointer, a hook

Theory-

When a load F suspended from lower free and of a spring handing from a rigid support, increases its length by amount I.

Then F I

F= KI

Where k is constant of proportionality. It is called the force constant or the spring constant of the spring.

From above if I = 1, F = K

Hence force constant (or spring constant) of a spring may be defined as the force required to produce unit extension in the spring.

Observations-

Least count of vertical scale = 0.1cm

Observation Table-

S. No. of observations	Load in Hanger (W) = Applied force (F) gwt.	Reading of position of pointer tip			Extension (cm)
S. No. of observations	Load in Hanger (W) = Applied force (F) gwt.	Load increasing x (cm)	Load decreasing Y (cm)	Mean = $\displaystyle \frac{{X+Y}}{2}$ (cm)	Extension (cm)
1
2
3
4
5
6

Calculations –

K_avg = $\displaystyle \frac{{{{K}_{1}}+{{K}_{2}}+{{K}_{3}}+{{K}_{4}}+{{K}_{5}}}}{5}$

K_avg = …………….g wt /cm

Result –

The spring constant or the force constant of the given spring is …………g wt per cm.

Precautios –

Loading and unloading of weight must be only gently.
Reading should be taken only when tip of pointer comes to rest.

Sources of error-

Support may not be rigid.
The slotted weight may not have corrected weight. (20g).

Experiment – 4

Aim –

To study the relationship between the temperature of a hot body and time by plotting a cooling curve.

Apparatus –

Newton’s law of cooling apparatus (a thin walled copper calorimeter suspended in a double walled enclosure) thermometer, clamp and stand, stop watch.

Theory –

From Newton’s law of cooling

Rate of cooling μ difference of temperature q kept in surrounding of temperature q₀

Rate of cooling $\displaystyle \frac{{d\theta }}{{dt}}=-ms\frac{{d\theta }}{{dt}}$

Hence, $\displaystyle \frac{{d\theta }}{{dt}}\alpha \left( {\theta -{{\theta }_{0}}} \right)$ → $\displaystyle \frac{{d\theta }}{{dt}}$ = $\displaystyle k\left( {\theta -{{\theta }_{0}}} \right)$ (ms = constant)

As time increases ; θ decreases ; (θ – θ₀) decreases hence rate of fall of temperature $\displaystyle \frac{{d\theta }}{{dt}}$ must also decrease

Observations –

Least count of thermometer = 1.0⁰C

Table for time and temperature –

S. No.	Time for cooling t (s)	Temperature of water in calorimeter θ ( ⁰C)	Temperature of water in enclosure Θ₀ ( ⁰C)	Difference of Temperature Θ – Θ₀ ( ⁰C)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Result –

The temperature falls quickly in the beginning and then slowly as difference of temperature goes on decreasing

This is in agreement with Newton’s law of cooling.

Precautions –

Double – walled enclosure should be used to maintain surrounding at a constant temperature.
Stirring should remain continuous for uniform cooling.

Sources of Error –

Surrounding temperature may change

Experiment-5

Aim –

To determine the time period of a simple pendulum for different lengths.
To plot the L – T and L – T² graphs from the above data and determine the length of the pendulum having one second as the time period.
To find the length of a second’s pendulum.

Apparatus Required–

A small metallic sphere with a hook, inextensible thread (about 1.5 m long), a tall stand with clamp, a split cork, vernier calliper, meter rod and stop clock.

Theory –

The time period ‘T’ of a simple pendulum of length ‘L’ is given by the relation :

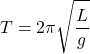$\displaystyle T=2\pi \sqrt{{\frac{L}{g}}}$ ……………………………………(1)

Squaring both sides and on rearranging

$\displaystyle G=\frac{{4{{\pi }^{2}}L}}{2}$ ………………………………(2)

Equation (2) suggests that the avg. value of $\displaystyle \frac{L}{{{{T}^{2}}}}$ when multiplied by $\displaystyle 4{{\pi }^{2}}$ would give the value of g at the place of experiment.

The best way of obtaining the average of L/T² is:

To draw a graph between L and T². The graph will be a straight line.
The slopw of L vs. T² graph plotted by taking L along y-axis and along x-axis gives average value of $\displaystyle \frac{L}{{{{T}^{2}}}}$

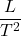
Observation –

Radius of the bob + length of the hook = = 2.5cm

Observation table –

Time period of simple pendulum for its different lengths –

S. No.	Length of Thread (cm)	Effective length of pendulum L = l+ (cm)	Time for 10 oscillation (s) (t₁)	Time period T₁ (S) T₁ = $\displaystyle \frac{{{{t}_{1}}}}{{10}}$	Time for 20 oscillations (s) (t₂) T₁ = $\displaystyle \frac{{{{t}_{2}}}}{{10}}$	Mean time T = $\displaystyle \frac{{{{T}_{1}}+{{T}_{2}}}}{{10}}$ 0	T²
1
2
3
4
5
6

Calculation-

Percentage Error in L_eff

= $\displaystyle \frac{{\text{Experimental Value - Standard Value}}}{{\text{Standard Value}}}\times 100$

= ………….%

Result –

Time period of simple pendulum of different lengths is measured.
L – T and L-T² graphs are plotted

Length of pendulum having time period 1 s is

= ………..cm

Length of second’s pendulum = ………….cm

Percentage error = ………%

Precautions –

An inextensible and strong thread should be used for making the pendulum.
A rigid support be used for suspending the pendulum.
The lower faces of the split cork should lie in the same horizontal plane.
The amplitude of oscillation should be kept small otherwise the relation $\displaystyle T=2\pi \sqrt{{\frac{L}{g}}}$

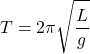
would not hold good.

As far as possible, the bob should be allowed to oscillate in the same vertical plane and any spinning or up and down motion of the bob must be avoided
The experiment should be performed at a place which is free any air disturbances, even the fan should be switch off.

Sources of Error –

The suspension support may not be rigid.
Sometimes it becomes difficult to avoid conical motion of the bob of the pendulum.
Some personal error is always involved in the starting and stopping of the stop watch.
Air blow cannot be completely eliminated.
Elasticity of the string always causes some error.

Experiment -6

Aim
To study the relation between frequency and length of a given wire under constant tension using sonometer.

Apparatus
A sonometer, a set of eight tuning forks, 1\2 kg hanger, five 1\2 kg slotted weights, rubber pad, paper rider, metre scale, screw gauge.

Diagram

Theory –
If stretched wire (string) vibrates in resonance with a tuning fork of frequency v, then the string also has same frequency v.
If the string has a length l, diameter D, material of density p and tension T, then

$\displaystyle {{v}_{0}}=\frac{1}{{2l}}\sqrt{{\frac{T}{m}}}$ ……………..(1)

Relation between frequency (v) and length (l). From Equation (1) above, $\displaystyle v\alpha \frac{1}{l}$

vl = constant,

A graph between v and $\displaystyle \frac{1}{l}$ will be straight line, while a graph between v and l will be a rectangular hyperbola.

Observation –

Constant tension on the wire T = 2.5kg

Observation Table-

S.No.	Frequency of tuning forl used (Hz)	Resonant Length Increasing l₁ (cm)	Resonant Length decreasing l₂ (cm	Resonant mean Length $\displaystyle \frac{{{{l}_{1}}+{{l}_{2}}}}{2}$ = (cm)	$\displaystyle \frac{1}{l}$ (cm^-1)
1
2
3
4
5

Result –

(i) A graph is plotted between v and $\displaystyle \frac{1}{l}$ which is straight line, &

(ii) A graph is plotted between v and l which is rectangular hyperbola.

Fom the graph we conclude that vl = constant i.e.

$\displaystyle v\alpha \frac{1}{l}$

This verifies law of length of transverse vibration of string

Precaution –

The edges of the wedges used may not be sharp.
Some friction might be present at the pulley and hence the tension is less than that actually applied.

Sources of Error –

The relationship has been derived under the condition that the wire is perfectly flexible. Hence an error may creep in due to rigidity of the wire.
The wires may not be of uniform are of cross-section or their compositions may not be uniform.

Practical of Physics Class 11

Leave a Reply Cancel reply