CBSE Important Question of Inverse Trigonometric Functions Class 12 Maths

MCQ WITH ANSWER

One branch of $\displaystyle {{\cos }^{{-1}}}x$ other than the principal value branch corresponds to:

(a) $\displaystyle \left[ {\frac{\pi }{2},\frac{{3\pi }}{2}} \right]$

(b) $\displaystyle \left[ {\pi ,2\pi } \right]-\left\{ {\frac{{3\pi }}{2}} \right\}$

(d) [2π, 3π]

Ans . (d)

The principal value of $\displaystyle \left[ {\pi ,2\pi } \right]-\left\{ {\frac{{3\pi }}{2}} \right\}$ is

(a) $\displaystyle \frac{{2\pi }}{9}$

(b) $\displaystyle -\frac{{2\pi }}{9}$

(d) $\displaystyle \frac{\pi }{9}$

Ans. (a )

3. If $\displaystyle {{\cos }^{{-1}}}x-{{\sin }^{{-1}}}x=0$ then the value of x is:

(a) 0

(b) 1

(d) $\displaystyle \frac{{\sqrt{3}}}{2}$

Ans. (c)

4. The value of $\displaystyle {{\cos }^{{-1}}}\left( {\cos \left( {\frac{{13\pi }}{6}} \right)} \right)$

(a) $\displaystyle \frac{{13\pi }}{6}$

(b) $\displaystyle \frac{{7\pi }}{6}$

(d) $\displaystyle \frac{\pi }{6}$

Ans.(d)

5. The value of $\displaystyle {{\sin }^{{-1}}}\left( {\frac{1}{2}} \right)+2{{\cos }^{{-1}}}\left( {\frac{{-\sqrt{3}}}{2}} \right)$ is

(a) $\displaystyle \frac{\pi }{2}$

(b) $\displaystyle -\frac{\pi }{2}$

(d)none of these

Ans. (d)

ONE MARK QUESTIONS WITH ANSWERS

1. the value of $\displaystyle {{\sin }^{{-1}}}\left( {\sin \frac{{3\pi }}{5}} \right)$ .

Ans . $\displaystyle {\frac{{2\pi }}{5}}$

2. Evaluate $\displaystyle {{\cos }^{{-1}}}\left( {\cos \frac{{7\pi }}{6}} \right)$

Ans. $\displaystyle {\frac{{5\pi }}{6}}$

3. Which is greater tan1 or tan^-1 .

Ans. tan¹ > tan^-1

4. $\displaystyle {{\sin }^{{-1}}}\left( {\sin \left( {\frac{{2\pi }}{3}} \right)} \right)=\frac{{2\pi }}{3}$ state true or false.

Ans. False

5. Domain of function sin^-1x is (-1,1), state true or false.

Ans. False

6. If $\displaystyle {{\tan }^{{-1}}}x={{\sin }^{{-1}}}\frac{1}{{\sqrt{2}}}$ , then x is …….

Ans. 1

7. Find the value of $\displaystyle \cot \left( {{{{\tan }}^{{-1}}}a+{{{\cot }}^{{-1}}}a} \right)$

Ans. 0

Assertion- Reason Question

Assertion(A): Principal value branch of x is $\displaystyle \left[ {-\frac{\pi }{2},\frac{\pi }{2}} \right]$

Reason(R): In this branch the function is bijective

Both A and R are true and R is the correct explanation for A.
Both A and R are true and R is not the correct explanation for A.

(d) A is false but R is true.

Ans: (b)

THREE LEVELS OF GRADED QUESTIONS

Level I (Very Short Type Question)

1. Find the principal value of $\displaystyle {{\sin }^{{-1}}}\left( {\frac{{-1}}{2}} \right)$

Ans $\displaystyle -\frac{\pi }{6}$

2. Find the principal value of $\displaystyle {{\cos }^{{-1}}}\left( {\frac{{\sqrt{3}}}{2}} \right)$

Ans $\displaystyle \frac{\pi }{6}$

3. Find the principal value of $\displaystyle {{\tan }^{{-1}}}\left( {-\sqrt{3}} \right)$

Ans $\displaystyle \frac{{4\pi }}{3}$ .

4. Find the value of $\displaystyle {{\tan }^{{-1}}}\left( 1 \right)+{{\sin }^{{-1}}}\left( {\frac{{-1}}{2}} \right)$ .

Ans $\displaystyle \frac{\pi }{{12}}$

5. Find the value of $\displaystyle {{\tan }^{{-1}}}\left( {\sqrt{3}} \right)-{{\cot }^{{-1}}}\left( {-\sqrt{3}} \right)$ .

Ans $\displaystyle \frac{\pi }{{12}}$

6. Find the value of $\displaystyle \sin \left( {\frac{\pi }{3}-{{{\sin }}^{{-1}}}\left( {\frac{{-1}}{2}} \right)} \right)$

Ans 1

7. Find the principal value of $\displaystyle {{\tan }^{{-1}}}\sqrt{3}-{{\sec }^{{-1}}}\left( {-2} \right)$

Ans $\displaystyle \frac{\pi }{3}$

Level Il (SHORT TYPE QUESTION)

1. Find the value of $\displaystyle {{\tan }^{{-1}}}\left( 1 \right)+{{\cos }^{{-1}}}\left( {\frac{{-1}}{2}} \right)+{{\sin }^{{-1}}}\left( {\frac{{-1}}{2}} \right)$

Ans $\displaystyle \frac{{3\pi }}{4}$

2. Find the value of $\displaystyle \tan \left\{ {{{{\sin }}^{{-1}}}\left( {\frac{3}{5}} \right)+{{{\cot }}^{{-1}}}\left( {\frac{3}{2}} \right)} \right\}$

Ans $\displaystyle \frac{{17}}{6}$

3. Write in simplest form: $\displaystyle \tan \left( {\frac{{\cos x-\sin x}}{{\cos x+\sin x}}} \right)$

Ans $\displaystyle \frac{\pi }{4}x$

4. Show that $\displaystyle {{\sin }^{{-1}}}\left( {\frac{3}{5}} \right)+-{{\sin }^{{-1}}}\left( {\frac{8}{{17}}} \right)={{\cos }^{{-1}}}\left( {\frac{{84}}{{85}}} \right)$

5. prove that $\displaystyle {{\cot }^{{-1}}}\left[ {\frac{{\sqrt{{1+\sin x}}+\sqrt{{1-\sin x}}}}{{\sqrt{{1+\sin x}}-\sqrt{{1-\sin x}}}}} \right]=\frac{x}{2}$ , 0<x< $\displaystyle \frac{\pi }{2}$

6. Prove that $\displaystyle {{\tan }^{{-1}}}\left( x \right)+{{\tan }^{{-1}}}\left( {\frac{{2x}}{{1-{{x}^{2}}}}} \right)={{\tan }^{{-1}}}\left( {\frac{{3x-{{x}^{3}}}}{{1-3{{x}^{2}}}}} \right)$

Level III (Long Type Question)

1. If $\displaystyle {{\sin }^{{-1}}}\left( {1-x} \right)-2{{\sin }^{{-1}}}x=\frac{\pi }{2}$ find the value of x.

2. Show that $\displaystyle {{\sin }^{{-1}}}\frac{{12}}{{13}}+{{\cos }^{{-1}}}\frac{4}{5}+{{\tan }^{{-1}}}\frac{{63}}{{60}}=\pi$

3. If $\displaystyle {{\tan }^{{-1}}}x+{{\tan }^{{-1}}}y+{{\tan }^{{-1}}}z=\frac{\pi }{2}$ , then show that xy+yz+zx=l

4. Prove that $\displaystyle \cos \left( {{{{\sin }}^{{-1}}}\frac{3}{5}+{{{\cot }}^{{-1}}}\frac{3}{2}} \right)=\frac{6}{{5\sqrt{{13}}}}$

5. Solve: $\displaystyle \cos \left( {{{{\tan }}^{{-1}}}x} \right)=\sin \left( {{{{\cot }}^{{-1}}}\frac{3}{4}} \right)$

6. Simplify: $\displaystyle {{\sin }^{{-1}}}\left( {\frac{{3x+4\sqrt{{1-{{x}^{2}}}}}}{5}} \right)$

7. Prove that $\displaystyle \left[ {{{{\cot }}^{{-1}}}\left\{ {\cos \left( {{{{\tan }}^{{-1}}}x} \right)} \right\}} \right]=\sqrt{{\frac{{\left( {{{x}^{2}}+1} \right)}}{{\left( {{{x}^{2}}-1} \right)}}}}$

8. If $\displaystyle {{\tan }^{{-1}}}a+{{\tan }^{{-1}}}b+{{\tan }^{{-1}}}c=\pi$ prove that a + b + c = abc

Case based Question

Two men on either side of a temple of 30 m high observe its top at the angles of elevation a and ß respectively,

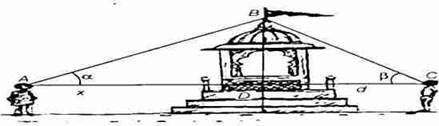
The distance between the two men is $\displaystyle 40\sqrt{3}$ m and the distance between the first person A and the temple is $\displaystyle 30\sqrt{3}$ m.

Answer the following questions using the above information.

(i) ∠CAB = α =

(a) $\displaystyle \left( {\frac{2}{{\sqrt{3}}}} \right)$ (b) $\displaystyle \left( {\frac{1}{2}} \right)$ (c) 2 (d) $\displaystyle \left( {\frac{{\sqrt{3}}}{2}} \right)$

(ii) ∠CAB = α =

(a) $\displaystyle \left( {\frac{1}{5}} \right)$ (b) $\displaystyle \left( {\frac{2}{5}} \right)$ (c) $\displaystyle \left( {\frac{4}{5}} \right)$ (d) $\displaystyle \left( {\frac{{\sqrt{3}}}{2}} \right)$

(iii) ∠BCA = β =

(a) $\displaystyle \left( {\frac{1}{2}} \right)$ (b) 2 (c) $\displaystyle \left( {\frac{1}{{\sqrt{3}}}} \right)$ (d) $\displaystyle \left( {\sqrt{3}} \right)$

(iv) ∠ABC =

(a) $\displaystyle \frac{\pi }{4}$ (b) $\displaystyle \frac{\pi }{6}$ (c) $\displaystyle \frac{\pi }{2}$ (d) $\displaystyle \frac{\pi }{3}$

Ans:. (i) (b) (ii) (d) (iii) (d) (iv) (c)

CBSE Important Question of Inverse Trigonometric Functions Class 12 Maths

Case based Question

Leave a Reply Cancel reply