Applications of Derivatives EXERCISE 6.1

Chapter 6 Applications of Derivatives

EXERCISE 6.1

Question 1: Find the rate of change of the area of a circle with respect to its radius r when

(a) r = 3 cm (b) r = 4 cm

Solution:

We know that the area of a circle, A = πr³

Therefore, the rate of change of the area with respect to its radius is given by

$\displaystyle \frac{{dA}}{{dr}}=\frac{d}{{dr}}\left( {\pi {{r}^{2}}} \right)$

= 2πr

When r = 3 cm

Then,

$\displaystyle \frac{{dA}}{{dr}}=2\pi \left( 3 \right)$

= 6 π

Thus, the area is changing at the rate of 6π.

When r = 4 cm

Then,

$\displaystyle \frac{{dA}}{{dr}}=2\pi \left( 4 \right)$

= 8π

Thus, the area is changing at the rate of 8π .

Question 2: The volume of a cube is increasing at the rate of 8 cm³/s . How fast is the surface area increasing when the length of its edge is 12 cm?

Solution:

Let the side length, volume and surface area respectively be equal to, x, V and S.

Hence, V = x³ and S = 6x²

We have,

$\displaystyle \frac{{dV}}{{dt}}=dc{{m}^{3}}/s$

Therefore,

$\displaystyle \frac{{dV}}{{dt}}=\frac{d}{{dt}}\left( {{{x}^{3}}} \right)$

$\displaystyle 8=\frac{d}{{dx}}\left( {{{x}^{3}}} \right)\frac{{dx}}{{dt}}$

$\displaystyle 8=3{{x}^{2}}\frac{{dx}}{{dt}}$

$\displaystyle \frac{{dx}}{{dt}}=\frac{8}{{3{{x}^{2}}}}$ ……………………(1)

Now,

$\displaystyle \frac{{dS}}{{dt}}=\frac{d}{{dt}}\left( {6{{x}^{2}}} \right)$

$\displaystyle \frac{{dS}}{{dt}}=\frac{d}{{dx}}\left( {6{{x}^{2}}} \right)\frac{{dx}}{{dt}}$

$\displaystyle \frac{{dS}}{{dt}}=12x\frac{{dx}}{{dt}}$

$\displaystyle \frac{{dS}}{{dt}}=12x\left( {\frac{8}{{3{{x}^{2}}}}} \right)$

From (1)

$\displaystyle \frac{{dS}}{{dt}}=\frac{{32}}{x}$

So, when x = 12 cm

Then,

$\displaystyle \frac{{dS}}{{dt}}=\frac{{32}}{{12}}=\frac{8}{3}c{{m}^{2}}/s$

Question 3: The radius of a circle is increasing uniformly at the rate of 3cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm/s.

Solution:

We know that A = πr²

Now,

$\displaystyle \frac{{dA}}{{dt}}=\frac{d}{{dr}}\left( {\pi {{r}^{2}}} \right)$

$\displaystyle \frac{{dA}}{{dt}}=2\pi r\frac{{dr}}{{dt}}$

We have,

$\displaystyle \frac{{dr}}{{dt}}=3cm/s$

$\displaystyle \frac{{dA}}{{dt}}=2\pi r\left( 3 \right)$ = 6πr

So, when r = 10 cm

Then,

$\displaystyle \frac{{dA}}{{dt}}=6\pi \left( {10} \right)$

= 60π cm²/s

Question 4: An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10cm long?

Solution:

Let the length and the volume of the cube respectively be x and V.

Hence, V = x³

Now,

$\displaystyle \frac{{dV}}{{dt}}=\frac{d}{{dt}}\left( {{{x}^{3}}} \right)$

$\displaystyle \frac{{dV}}{{dt}}=\frac{d}{{dx}}\left( {{{x}^{3}}} \right)\frac{{dx}}{{dt}}$

$\displaystyle \frac{{dV}}{{dt}}=3{{x}^{2}}\frac{{dx}}{{dt}}$

We have,

$\displaystyle \frac{{dx}}{{dt}}=3cm/s$

Hence,

$\displaystyle \frac{{dV}}{{dt}}=3{{x}^{2}}\left( 3 \right)$ = 9x²

So, when x = 10 cm

Then,

$\displaystyle \frac{{dV}}{{dt}}=9{{\left( {10} \right)}^{2}}$

= 300 cm³/s

Question 5: A stone is dropped into a quiet lake and waves move in circles at the speed of 5cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the encoding area is increasing?

Solution:

We know that A = πr²

Now,

$\displaystyle \frac{{dA}}{{dt}}=\frac{d}{{dt}}\left( {\pi {{r}^{2}}} \right)$

$\displaystyle \frac{{dA}}{{dt}}=2\pi r\frac{{dr}}{{dt}}$

We have,

$\displaystyle \frac{{dr}}{{dt}}=5cm/s$

Hence,

$\displaystyle \frac{{dA}}{{dt}}=2\pi r\left( 5 \right)$

= 10πr

So, when r=8cm

Then,

$\displaystyle \frac{{dA}}{{dt}}=10\pi \left( 8 \right)$

= 80π cm²/s

Question 6: The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?

Solution:

We know that C = 2πr

Now,

$\displaystyle \frac{{dC}}{{dt}}=\frac{d}{{dt}}\left( {2\pi r} \right)$

$\displaystyle =\frac{d}{{dr}}\left( {2\pi r} \right)\frac{{dr}}{{dt}}$

$\displaystyle =2\pi \frac{{dr}}{{dt}}$

We have,

$\displaystyle \frac{{dr}}{{dt}}=0.7\pi cm/s$

Hence,

$\displaystyle \frac{{dC}}{{dt}}=2\pi \left( {0.7} \right)$ = 1.4π cm/s

Question 7: The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/ minute. When x = 8cm and y = 6 cm, find the rate of change of (a) the perimeter and (b) the area of the rectangle.

Solution:

It is given that $\displaystyle \frac{{dx}}{{dt}}=-5cm/\min ute$ and $\displaystyle \frac{{dx}}{{dt}}=4cm/\min ute$ and x = 8 cm and y = 6 cm

(a) The perimeter of a rectangle is given by P = 2(x+y) cm

Therefore,

$\displaystyle \frac{{dP}}{{dt}}=2\left( {\frac{{dx}}{{dt}}+\frac{{dy}}{{dt}}} \right)$

= $\displaystyle 2\left( {-5+4} \right)=-2$ cm/ minute

(b) The area of a rectangle is given by A = xy

Therefore,

$\displaystyle \frac{{dA}}{{dt}}=\frac{{dx}}{{dt}}y+\frac{{dy}}{{dt}}x$

= $\displaystyle -5y+4x$

When x = 8 cm and y = 6 cm

Then,

$\displaystyle \frac{{dA}}{{dt}}=\left( {-5\times 6+4\times 8} \right)$ cm²/minute

= 2 cm²/ minute

Question 8: A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15cm.

Solution:

V = $\displaystyle \frac{4}{3}\pi {{r}^{3}}$

Hence,

$\displaystyle \frac{{dV}}{{dt}}=\frac{d}{{dr}}\left( {\frac{4}{3}\pi {{r}^{3}}} \right)\frac{{dr}}{{dt}}$

= $\displaystyle 4\pi {{r}^{2}}\frac{{dr}}{{dt}}$

We have,

$\displaystyle \frac{{dV}}{{dr}}=900c{{m}^{2}}/s$

Therefore,

$\displaystyle 4\pi {{r}^{2}}\frac{{dr}}{{dt}}=900$

$\displaystyle \frac{{dr}}{{dt}}=\frac{{900}}{{4\pi {{r}^{2}}}}$

= $\displaystyle \frac{{225}}{{\pi {{r}^{2}}}}$

When radius, r = 15 cm

Then,

$\displaystyle \frac{{dr}}{{dt}}=\frac{{225}}{{\pi {{{\left( {15} \right)}}^{2}}}}$

= $\displaystyle \frac{1}{\pi }cm/s$

Question 9: A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the latter is 10cm.

Solution:

We know that V= $\displaystyle \frac{4}{3}\pi {{r}^{3}}$

Therefore,

$\displaystyle \frac{{dV}}{{dr}}=\frac{d}{{dr}}\left( {\frac{4}{3}\pi {{r}^{3}}} \right)$

= $\displaystyle \frac{4}{3}\pi \left( {3{{r}^{2}}} \right)$

= 4πr²

When radius, r = 10 cm

Then,

$\displaystyle \frac{{dV}}{{dt}}=4\pi {{\left( {10} \right)}^{2}}$

= 400 π

Thus, the volume of the balloon is increasing at the rate of 400π cm³/s.

Question 10: A ladder is 5m long is leaning against the wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4m away from the wall?

Solution:

Let the height of the wall at which the ladder is touching it be y m and the distance of its foot from the wall on the ground be x m.

Hence,

$\displaystyle {{x}^{2}}+{{y}^{2}}={{5}^{2}}$

$\displaystyle \Rightarrow {{y}^{2}}=25-{{x}^{2}}$

$\displaystyle \Rightarrow y=\sqrt{{25-{{x}^{2}}}}$

Therefore,

$\displaystyle \frac{{dy}}{{dt}}=\frac{d}{{dt}}\left( {\sqrt{{25-{{x}^{2}}}}} \right)$

= $\displaystyle \frac{d}{{dx}}\left( {\sqrt{{25-{{x}^{2}}}}} \right)\frac{{dx}}{{dt}}$

= $\displaystyle \frac{{-x}}{{\left( {\sqrt{{25-{{x}^{2}}}}} \right)}}\frac{{dx}}{{dt}}$

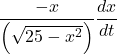
We have,

$\displaystyle \frac{{dx}}{{dt}}=2cm/s$

Thus,

$\displaystyle \frac{{dy}}{{dt}}=\frac{{-2x}}{{\left( {\sqrt{{25-{{x}^{2}}}}} \right)}}$

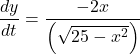
When x = 4 cm

Then,

$\displaystyle \frac{{dy}}{{dt}}=\frac{{-2\times 4}}{{\left( {\sqrt{{25-{{4}^{2}}}}} \right)}}$

$\displaystyle \frac{{dy}}{{dt}}=\frac{{-8}}{{\left( {\sqrt{{25-16}}} \right)}}$

$\displaystyle \frac{{dy}}{{dt}}=\frac{{-8}}{{\left( {\sqrt{9}} \right)}}$

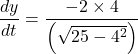
$\displaystyle \frac{{dy}}{{dt}}=\frac{{-8}}{3}$ cm/s

Question 11: A particle is moving along the curve 6y = x³+ 2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.

Solution:

The equation of the curve is 6y = x³+ 2

Differentiating with respect to time, we have

$\displaystyle 6\frac{{dy}}{{dt}}=3{{x}^{2}}\frac{{dx}}{{dt}}$

$\displaystyle 2\frac{{dy}}{{dt}}={{x}^{2}}\frac{{dx}}{{dt}}$

According to the question, $\displaystyle \left( {\frac{{dy}}{{dt}}=8\frac{{dx}}{{dt}}} \right)$

Hence,

$\displaystyle \Rightarrow 2\left( {8\frac{{dx}}{{dt}}} \right)={{x}^{2}}\frac{{dx}}{{dt}}$

$\displaystyle \Rightarrow 16\frac{{dx}}{{dt}}={{x}^{2}}\frac{{dx}}{{dt}}$

$\displaystyle \Rightarrow \left( {{{x}^{2}}-16} \right)\frac{{dx}}{{dt}}=0$

$\displaystyle \Rightarrow {{x}^{2}}=16$

$\displaystyle \Rightarrow x=\pm 4$

When x = 4

Then,

$\displaystyle y=\frac{{{{4}^{3}}+2}}{6}$

= $\displaystyle \frac{{66}}{6}$ = 11

When x = – 4

Then,

$\displaystyle y=\frac{{{{{\left( {-4} \right)}}^{3}}+2}}{6}$

$\displaystyle y=\frac{{-64+2}}{6}$

$\displaystyle y=\frac{{-62}}{6}$

$\displaystyle y=\frac{{-31}}{3}$

Thus, the points on the curve are (4, 11) and $\displaystyle \left( {-4,\frac{{-31}}{3}} \right)$ .

Question 12: The radius of an air bubble is increasing at the rate of $\displaystyle \frac{1}{2}$ cm/s. At which rate is the volume of the bubble increasing when the radius is 1cm?

Solution:

Assuming that the air bubble is a sphere, V = $\displaystyle \frac{4}{3}\pi {{r}^{3}}$ Therefore,

$\displaystyle \frac{{dV}}{{dt}}=\frac{d}{{dt}}\left( {\frac{4}{3}\pi {{r}^{3}}} \right)\frac{{dr}}{{dt}}$

= $\displaystyle 4\pi {{r}^{2}}\frac{{dr}}{{dt}}$

We have,

$\displaystyle \frac{{dr}}{{dt}}=\frac{1}{2}cm/s$

When r= 1 cm

Then,

$\displaystyle \frac{{dV}}{{dt}}=4\pi {{\left( 1 \right)}^{2}}\left( {\frac{1}{2}} \right)$

= 2π cm³/s

Question 13: A balloon, which always remains spherical, has a variable diameter $\displaystyle \frac{3}{2}\left( {2x+1} \right)$ . Find the rate of change of its volume with respect to x.

Solution:

We know that $\displaystyle \frac{4}{3}\pi {{r}^{3}}$

It is given that diameter, $\displaystyle d=\frac{3}{2}\left( {2x+1} \right)$

Hence, $\displaystyle r=\frac{3}{4}\left( {2x+1} \right)$

Therefore,

V = $\displaystyle \frac{4}{3}\pi {{\left( {\frac{3}{4}} \right)}^{3}}{{\left( {2x+1} \right)}^{3}}$

= $\displaystyle \frac{9}{{16}}\pi {{\left( {2x+1} \right)}^{3}}$

Thus,

$\displaystyle \frac{{dV}}{{dx}}=\frac{9}{{16}}\pi \frac{d}{{dx}}{{\left( {2x+1} \right)}^{3}}$

= $\displaystyle \frac{{27}}{8}\pi {{\left( {2x+1} \right)}^{3}}$

Question 14: Sand is pouring from a pipe at the rate of 12 cm³/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when height is 4 cm?

Solution:

We know that V = $\displaystyle \frac{1}{3}\pi {{r}^{2}}h$

It is given that, $\displaystyle h=\frac{1}{6}r$

Hence, r = 6h

Therefore,

V = $\displaystyle \frac{1}{3}\pi {{\left( {6h} \right)}^{2}}h$

= 12πh³

Thus,

$\displaystyle \frac{{dV}}{{dt}}=12\pi \frac{d}{{dt}}\left( {{{h}^{3}}} \right)\frac{{dh}}{{dt}}$

= $\displaystyle 12\pi \left( {3{{h}^{2}}} \right)\frac{{dh}}{{dt}}$

= $\displaystyle 36\pi {{h}^{2}}\frac{{dh}}{{dt}}$

We have, $\displaystyle \frac{{dV}}{{dt}}$ = 12 cm²/s

When h = 4 cm

Then,

12 = 36π(4)² $\displaystyle \frac{{dh}}{{dt}}$

$\displaystyle \frac{{dh}}{{dt}}=\frac{{12}}{{36\pi \left( {16} \right)}}$

= $\displaystyle \frac{1}{{48\pi }}$ cm/s

Question 13: The total cost C(x) in Rupees associated with the production of x units of an item is given by C(x) = 0.007 x³ – 0.003 x² + 15x + 4000. Find the marginal cost when 17 units are produced.

Solution: Marginal cost (MC) is the rate of change of the total cost with respect to the output. Therefore,

MC= $\displaystyle \frac{{dC}}{{dt}}$ = 0.007(3x²) – 0.003(2x) + 15

= 0.021 x² – 0.006 x + 15

When x = 17

Then,

MC = 0.021(17)2 – 0.006(17) + 15

= 0.021(289) – 0.006(17) + 16

= 6.069 – 0.102 + 15

= 20.967

So, when 17 units are produced, the marginal cost is ₹ 20.967.

Question 16: The total revenue in Rupees received from the sale of x units of a product given by R(x) = 13x² + 26x + 15. Find the marginal revenue when x = 7.

Solution:

Marginal revenue (MR) is the rate of change of the total revenue with respect to the number of units sold. Therefore,

MR = $\displaystyle \frac{{dR}}{{dx}}$ = 13(2x) + 26

When, x = 7

Then,

MR = 26(7) + 26 = 182 + 26 = 208

Thus, the marginal revenue is ₹ 208.

Question 17: The rate of change of the area of a circle with respect to its radius r at r = 6 cm is

10π (B) 12π (C) 8π (D) 11π

Solution:

We know that A = πr²

Therefore,

$\displaystyle \frac{{dA}}{{dr}}=\frac{d}{{dr}}\left( {\pi {{r}^{2}}} \right)$

= 2πr

When r = 6 cm

Then,

$\displaystyle \frac{{dA}}{{dr}}=2\pi \times 6$

= 12 π cm²/s

Thus, the rate of change of the area of the circle is 12 π cm²/s .

Hence, the correct option is B.

Question 18: The total revenue is Rupees received from the sale of x units of a product is given by R(x) = 3x² + 36x + 5. The marginal revenue, when x = 15 is

(A) 116 (B) 96 (C) 90 (D) 126

Solution:

Marginal revenue (MR) is the rate of change of the total revenue with respect to the number of units sold.

Therefore,

MR = $\displaystyle \frac{{dR}}{{dx}}$ = 3(2x) + 36

= 6x + 36

When, x = 15

Then,

MR = 6(15) + 36

= 90+36 = 126

Thus, the marginal revenue is ₹ 126.

Hence, the correct option is D.

Applications of Derivatives EXERCISE 6.1

Leave a Reply Cancel reply