EXERCISE 1.3
Question 1: Let f :{1,3,4} →{1,2,5}and g: {1,2,5} →{1,3} be given by f = {(1,2),(3,5),(4,1)} and g = {(1,3),(2,3),(5,1)}. Write down gof.
Solution: The functions f :{1,3,4} →{1,2,5}and g: {1,2,5} →{1,3} are f = {(1,2),(3,5),(4,1)} and g = {(1,3),(2,3),(5,1)}.
gof(1) = g [ f (1)] = g(2) = 3 [as f(1) = 2 and g(2)=3]
gof(3) = g [ f (3)] = g(5) = 1 [as f(3) = 5 and g(5)=1]
gof(4) = g [ f (4)] = g(1) = 3 [as f(4) = 1 and g(1)=3]
∴ gof = {(1,3),(3,1),(4,3)}
Question 2:
Let f, g, h be function form R to R. Show that
(f + g) oh = foh + goh
(f . g) oh = (foh) . (goh)
Solution:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\left[ {\left( {f+g} \right)oh} \right]x\\=\left( {f+g} \right)\left[ {h\left( x \right)} \right]=f\left[ {h\left( x \right)} \right]+g\left[ {h\left( x \right)} \right]\\=\left( {foh} \right)\left( x \right)+goh\left( x \right)\\=\left\{ {\left( {foh} \right)+\left( {goh} \right)} \right\}\left( x \right)=RHS\end{array}](https://gyanpoints.com/wp-content/ql-cache/quicklatex.com-34b80614a7090ab0a021557039c5c344_l3.png)
![]() for all x ∈ R
for all x ∈ R
Hence, ![]()
LHS = ![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\left[ {\left( {f.g} \right)oh} \right]\left( x \right)\\=\left( {f.g} \right)\left[ {h\left( x \right)} \right]=f\left[ {h\left( x \right).g\left( x \right)} \right]\\=\left( {foh} \right)\left( x \right).\left( {goh} \right)\left( x \right)\\=\left\{ {\left( {foh} \right).\left( {goh} \right)} \right\}\left( x \right)\end{array}](https://gyanpoints.com/wp-content/ql-cache/quicklatex.com-3a6591f7edde6908cfa0e4bb7250aa8b_l3.png) = RHS
= RHS
∴![]() for all x ∈ R
for all x ∈ R
Hence, ![]()
Question 3:
Find gof and fog, if
i. f (x) = ∣ x ∣ and g (x) = ∣5x – 2 ∣
ii. f (x) = 8x3 and g (x) = ![]()
Solution:
(i) f (x) = ∣ x ∣ and g (x) = ∣5x – 2 ∣
∴ ![]()
![]()
(ii) ![]() and
and ![]()
∴ ![]()
![]()
Question 4:
If ![]() , show that
, show that ![]() for all
for all ![]() . What is the reverse of f ?
. What is the reverse of f ?
Solution:
![]()
= 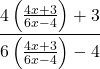
= ![]()
= ![]() = 34
= 34
∴fof (x) = x for all ![]()
fof = 1
Hence, the given function f is invertible and the inverse of f is f itself.
