EXERCISE 1.2

Question 1:

Show that the function $\displaystyle f:{{R}_{0}}\to {{R}_{0}}$ defined by $\displaystyle \left( x \right)=\frac{1}{x}$ is one –one and onto, where $\displaystyle {{R}_{0}}$ is the set of all non –zero real numbers. Is the result true, if the domain $\displaystyle {{R}_{0}}$ is replaced by N with codomain being same as $\displaystyle {{R}_{0}}$ ?

Solution:

$\displaystyle f:{{R}_{0}}\to {{R}_{0}}$ is by $\displaystyle f\left( x \right)=\frac{1}{x}$

For one-one:

$\displaystyle x,y\in {{R}_{0}}$ such that $\displaystyle f\left( x \right)=f\left( y \right)$

⇒ $\displaystyle \frac{1}{x}=\frac{1}{y}$

⇒ x = y

f is one-one.

For onto:

For $\displaystyle y\in R$ , there exists $\displaystyle x=\frac{1}{y}\in {{R}_{0}}\left[ {\text{as }y\in 0} \right]$ such that $\displaystyle f\left( x \right)=\frac{1}{{\frac{1}{y}}}=y$

f is onto.

Given function f is one-one and onto.

Consider function $\displaystyle g:N\to {{R}_{0}}$ defined by $\displaystyle g\left( x \right)=\frac{1}{x}$

$\displaystyle g\left( {{{x}_{1}}} \right)=f\left( {{{x}_{2}}} \right)$

⇒ $\displaystyle \frac{1}{{{{x}_{1}}}}=\frac{1}{{{{x}_{2}}}}$

⇒ $\displaystyle {{x}_{1}}={{x}_{2}}$

We have g is one-one

G is not onto as for $\displaystyle 1.2\in {{R}_{0}}$ there exist any x in N such that $\displaystyle g\left( x \right)=\frac{1}{{1.2}}$ function is one-one but not onto.

Question 2:

Check the injectivity and surjectivity of the following functions:

(i) $\displaystyle f:N\to N$ given by $\displaystyle f\left( x \right)={{x}^{2}}$

(ii) $\displaystyle f:Z\to Z$ given by $\displaystyle f\left( x \right)={{x}^{2}}$

(iii) $\displaystyle f:N\to N$ given by $\displaystyle f\left( x \right)={{x}^{3}}$

(iv) $\displaystyle f:Z\to Z$ given by $\displaystyle f\left( x \right)={{x}^{3}}$

Solution:

(i) For $\displaystyle f:N\to N$ given by $\displaystyle f\left( x \right)={{x}^{2}}$

x, y∈ N

f(x) = f(y) ⇒ x2 = y2 ⇒ x = y

∴ f is injective.

2∈N. But, there does not exist any x in N such that f(x) = x2 = 2

∴ f is not surjective

Function f is injective but not surjective.

(ii) f:Z→Z given by f(x) = x2

F(-1) = f(1) = 1 but -1 ≠ 1

∴ f is not injective.

-2 ∈ Z But, there does not exist any x ∈ Z such that f(x) = -2 ⇒ x2 = -2

∴ f is not surjective.

Function f is neither injective nor surjective.

(iii) $\displaystyle f:N\to N$ given by $\displaystyle f\left( x \right)={{x}^{3}}$

$\displaystyle f\left( {-1} \right)=f\left( 1 \right)$ but – 1 ≠ 1

∴ f is not injective.

-2 ∈ Z But, there does not exist any x ∈ Z such that f(x) = – 2 ⇒ x2 = -2

∴ f is not surjective

Function f is neither injective nor surjective.

(iv) $\displaystyle f:Z\to Z$ given by $\displaystyle f\left( x \right)={{x}^{3}}$

x, y ∈ N

f(x) = f(y) = x3 = y3 ⇒ x = y

∴ f is injective.

2 ∈ Z But, there does not exist any x ∈ Z such that f(x) = x3 = 2

∴ f is not surjective

Function f is neither injective nor surjective.

(iv) $\displaystyle f:Z\to Z$ given by $\displaystyle f\left( x \right)={{x}^{3}}$

x, y ∈ N

f(x) = f(y) = x3 = y3 ⇒ x = y

∴ f is injective.

2 ∈ Z But, there does not exist any x ∈ Z such that f(x) = x3 = 2

∴ f is not surjective

Function f is neither injective nor surjective.

Question 3:

Prove that the greatest integer function f:R→R given by $\displaystyle f\left( x \right)=\left[ x \right]$ is neither one-one nor onto, where $\displaystyle \left[ x \right]$ denotes the greatest integer less than or equal to x.

Solution:

$\displaystyle f:R\to R$ given by $\displaystyle f\left( x \right)=\left[ x \right]$

$\displaystyle f\left( {1.2} \right)=\left[ {1.2} \right]=1,f\left( {1.9} \right)=\left[ {1.9} \right]=1$

$\displaystyle \therefore f\left( {1.2} \right)=f\left( {1.9} \right)$ but 1.2 ≠ 1.9

∴ f is not one-one

Consider 0.7 ∈ R

f(x) = [x] is an integer. There does not exist any element x ∈R such that f(x) = 0.7

∴ f is not onto.

The greatest integer function is neither one-one nor onto.

Question 4:

Show that the modulus function f:R→R given by f(x) = ∣x∣ is neither one-one nor onto,

where ∣x∣ is x, if x is positive or and ∣x∣ is – x , if x is negative

Solution:

f: R→R is f(x) = ∣x∣ = $\displaystyle f\left( x \right)=\left| x \right|=\left\{ {\begin{array}{*{20}{c}} {x,ifx\ge 0} \\ {-x,ifx<0} \end{array}} \right.$

f(-1) = ∣-1∣ = 1 and f(1) = ∣1∣ = 1

f(-1) = f(1) but -1≠ 1

∴ f is not one-one.

Consider -1 ∈ R

f(x):∣x∣ is non-negative. There exist any element x in domain R such that f(x):∣x∣ = -1

∴ f is not onto.

The modulus function is neither one-one nor onto.

Question 5:

Show that the signum function f: R→R given by 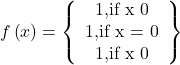$\displaystyle f\left( x \right)=\left\{ {\begin{array}{*{20}{c}} {\text{1,if x 0}} \\ {\text{1,if x = 0}} \\ {\text{1,if x 0}} \end{array}} \right\}$ is neither one-one nor onto.

Solution:

f: R→R is 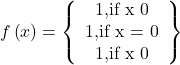$\displaystyle f\left( x \right)=\left\{ {\begin{array}{*{20}{c}} {\text{1,if x 0}} \\ {\text{1,if x = 0}} \\ {\text{1,if x 0}} \end{array}} \right\}$

f(1) = f(2) =1 but 1≠2

∴ f is not one-one.

f(x) takes only 3 values (1,0,1) for the element -2 in co-domain R, there does not exist any x in domain R such that f (x) = – 2.

∴ f is not onto.

The signum function is neither one-one nor onto.

Question 6:

Let A = {1,2,3}, B = {4,5,6,7}and let f = {(1,4),(2,5),(3,6)} be a function from A to B. Show that f is one-one.

Solution:

A = (1,2,3), B = {4,5,6,7}

f: A→B is defined as f = {(1,4),(2,5),(3,6)}

∴ f(1) = 4, f(2) = 5, f(3) = 6

It is seen that the images of distinct element of A under f are distinct.

∴ f is not one-one.

Question 7:

In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.

i. f:R→R defined by f(x) = 3 – 4x

ii. f:R→R defined by f(x) = 1 + x2

Solution:

(i) f:R→R defined by f(x) = 3 – 4x

x1, x2 ∈ R such that f(x1) = f(x2)

⇒ 3 – 4×1 = 3 – 4×2

⇒ – 4×1 = – 4×2

⇒ x1 = x2

∴ f is not one-one.

For any real number (y) in R, there exists $\displaystyle \frac{{3-y}}{4}$ in R such that $\displaystyle f\left( {\frac{{3-y}}{4}} \right)=3-4\left( {\frac{{3-y}}{4}} \right)=y$

∴ f is onto.

Hence, f is bijective.

ii. f:R→R defined by f(x) = 1 + x2

x1, x2 ∈ R such that f(x1) = f(x2)

⇒ $\displaystyle 1+x_{1}^{2}=1+x_{2}^{2}$

⇒ $\displaystyle x_{1}^{2}=x_{2}^{2}$

⇒ $\displaystyle {{x}_{1}}\pm {{x}_{2}}$

$\displaystyle \therefore f\left( {{{x}_{1}}} \right)=f\left( {{{x}_{2}}} \right)$ does not imply that x1 = x2.

Consider f(1) = f(-1) = 2

∴ f is not one-one.

Consider an element – 2 in co domain R.

It is seen that $\displaystyle f\left( x \right)=1+{{x}^{2}}$ is positive for all .

∴ f is not onto.

Hence, f is neither one-one nor onto.

Question 8:

Let A and B be sets. Show that $\displaystyle f:A\times B\to B\times A$ such that (a,b) = (b,a) is a bijective function.

Solution:

$\displaystyle f:A\times B\to B\times A$ is defined as (a,b) = (b,a).

$\displaystyle \left( {{{a}_{1}},{{b}_{1}}} \right),\left( {{{a}_{2}},{{b}_{2}}} \right)\in A\times B$ such that $\displaystyle f\left( {{{a}_{1}},{{b}_{1}}} \right)=f\left( {{{a}_{2}},{{b}_{2}}} \right)$

$\displaystyle \left( {{{a}_{1}},{{b}_{1}}} \right)=\left( {{{a}_{2}},{{b}_{2}}} \right)$

⇒ b1 = b2 and a1 = a2

⇒ (a1, b1) = (a2, b2)

∴ f is one-one.

(b, a) ∈ B × A there exist (a, b) ∈ A × B such that f(a, b) = (b, a)

∴ f is onto.

f is bijective.

Question 9:

Let f:N→N be defined as $\displaystyle f\left( n \right)=\left\{ {\begin{array}{*{20}{c}} {\frac{{n+1}}{2},if\text{ n is odd}} \\ {\frac{n}{2},if\text{ n is even}} \end{array}} \right\}$ for all n∈N. State whether the function is bijective. Justify your answer.

Solution:

f:N→N be defined as $\displaystyle f\left( n \right)=\left\{ {\begin{array}{*{20}{c}} {\frac{{n+1}}{2},if\text{ n is odd}} \\ {\frac{n}{2},if\text{ n is even}} \end{array}} \right\}$ for all n∈N.

$\displaystyle f\left( 1 \right)=\frac{{1+1}}{2}=1$ and $\displaystyle f\left( 2 \right)=\frac{2}{2}=1$

f(1) = f(2), where 1 ≠ 2

∴ f is not one-one.

Consider a natural number n in co domain N.

Case 1. n is odd

∴ n = 2r + 1 for some r ∈ N there exists 4r + 1 ∈ N such that

$\displaystyle f\left( {4r+1} \right)=\frac{{4r+1+1}}{2}=2r+1$

there exists 4r ∈ N such that

is not a bijective function.

Case 2. n is even

∴ n = 2r for some r ∈ N there exists 4r ∈ N such that

$\displaystyle f\left( {4r} \right)=\frac{{4r}}{2}=2r$

∴ f is onto.

∴ f is not a bijective function.

Question 10:

Let A = R – {3}, B = R – {1} and f:A→B defined by $\displaystyle f\left( x \right)=\left( {\frac{{x-2}}{{x-3}}} \right)$ . Is f one-one and onto?

Justify your answer.

Solution:

A = R – {3}, B = R – {1} and f:A→B defined by $\displaystyle f\left( x \right)=\left( {\frac{{x-2}}{{x-3}}} \right)$ .

x, y ∈ A such that f(x) = f(y)

⇒ $\displaystyle \frac{{x-2}}{{x-3}}=\frac{{y-2}}{{y-3}}$

⇒ (x-2)(y-3) = (y-2)(x-3)

⇒ xy – 3x – 2y + 6 = xy – 3y – 2x + 6

⇒ -3x – 2y = 3y – 2x

⇒ 3x – 2x = 3y – 2y

⇒ x = y

∴ f is one-one.

EXERCISE 1.2

Leave a Reply Cancel reply